PGADP数据驱动的优化控制

本文是对《Policy Gradient Adaptive Dynamic Programming for Data-Based Optimal Control》文章的整理归纳

期刊：《IEEE TRANSACTIONS ON CYBERNETICS》2019影响因子：11.079

这篇文章考虑了离散时间非线性系统的无模型的最优控制问题，提出了一个基于数据的策略梯度自适应动态规划算法（PGADP），使用离线和在线的数据而不是数学模型，使用梯度下降方法来改进策略，这篇文章还证明了PGADP算法的收敛性。

简介

最优控制问题一般需要求解一个复杂的Hamilton-Jacobi-Bellman equation，对于非线性系统，很难求出解析解，用ADP求解该方程在近年来取得了较大的成果。

主要分为三大类：

• model based：用ADP来近似求解HJBE
• partially model based：既用模型也用数据
• model free：模型未知，完全从数据中学习控制策略

问题描述

考虑如下非线性系统：

这篇文章考虑了model-free的最优控制方法，也就是说，除了知道该系统是Lipschitz连续的，该系统是完全未知的。

最优控制器设计的目标是：找到一个反馈控制率，使得该系统构成的闭环系统在平稳点是渐进稳定的，同时，使得以下无穷时域的cost function最小化：

其中，，和是正定矩阵。

优化问题可以描述成：

最优控制策略是：

策略梯度自适应动态规划算法

最优控制问题需要求解以下HJBE方程：

很显然，由于系统模型未知，解析解求不出来的。

给定一个容许控制策略：，定义它的状态价值函数，例如，可以采用上述定义的cost function作为它的状态价值函数：

从上式经过一步展开可以得到如下递推表达式:

最优的状态价值函数可以表示成:

再定义一个动作状态价值函数，或称为Q函数：

进一步可以写成：

Q函数表示：在状态下，执行动作后，计算出来的控制策略，所对应的性能指标值。

求得的最优控制策略是：

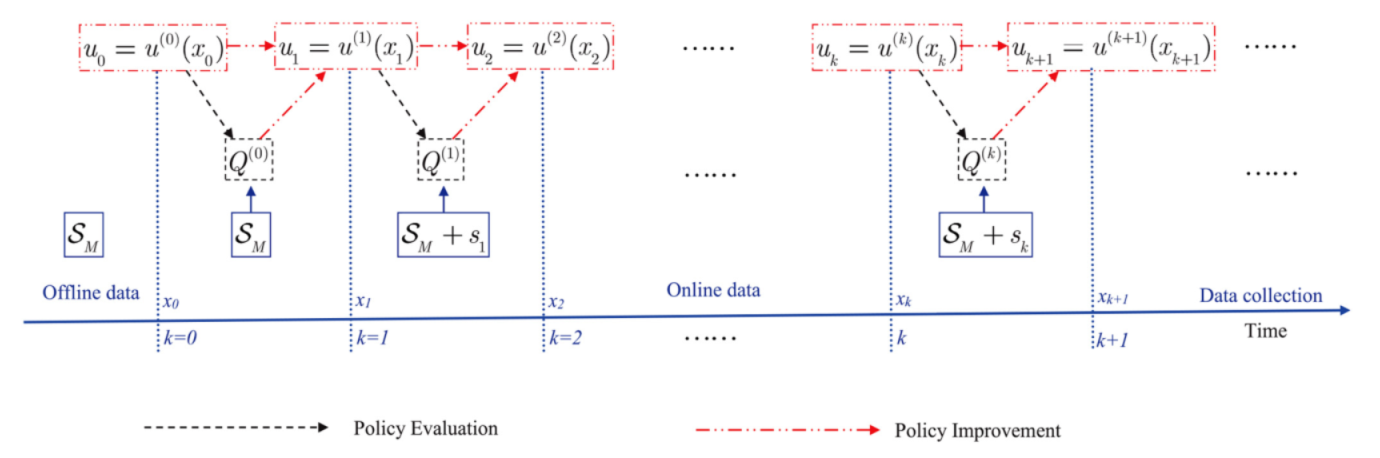
数据分为两部分：离线数据和在线数据

离线数据：

离线数据可以通过任意的控制约束集中的控制动作进行采样获得。

在线数据：

算法流程：

给定一个初始容许控制策略：

使用离线数据计算函数：

在时刻，将应用到被控系统中，并获得在线数据

通过Policy Improvement来求解

同样的，利用离线数据计算函数：

重复下去，直至收敛。

基于PGADP的actor-critic结构

仿真