强化学习之动态规划
复习了一下Sutton书中的第四章,动态规划,整理一下。
动态规划算法是所有强化学习算法的基础,所有强化学习算法都可以看作是为了得到和动态规划相同的效果,同时减少计算量和对环境模型的依赖。
这一章节主要分为三部分:策略评估,策略改进,策略迭代。
策略评估:对于一个给定的策略下,迭代地计算策略的价值函数。
策略改进:根据一个旧的策略的值函数,计算一个改进的策略。
将这两种方法结合起来,可以得到策略迭代算法和价值迭代算法。
强化学习算法的关键是使用价值函数来寻找到更加好的策略,首先定义价值函数,其满足Bellman最优性方程:
策略评估
目的:给定一个策略
如果环境动态是完全已知的,那么通过上述价值函数的表达式,可以列出

仿真算例:
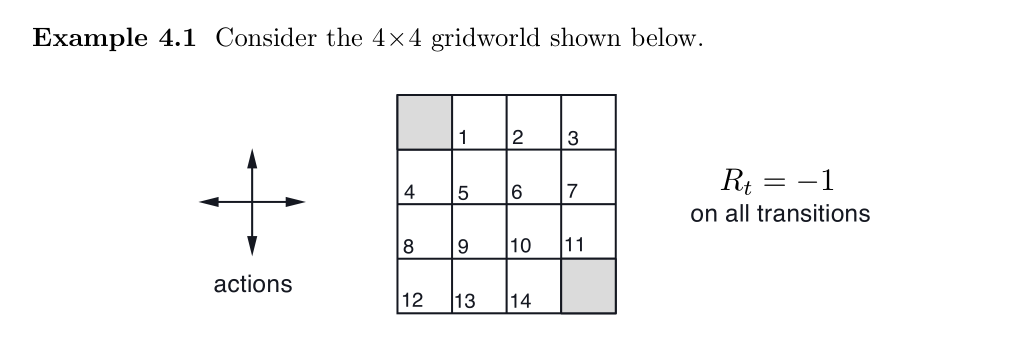
一个简单的额GridWorld的例子,通过不断迭代,即可算出所有的价值函数,代码:
1 | import numpy as np |
结果:
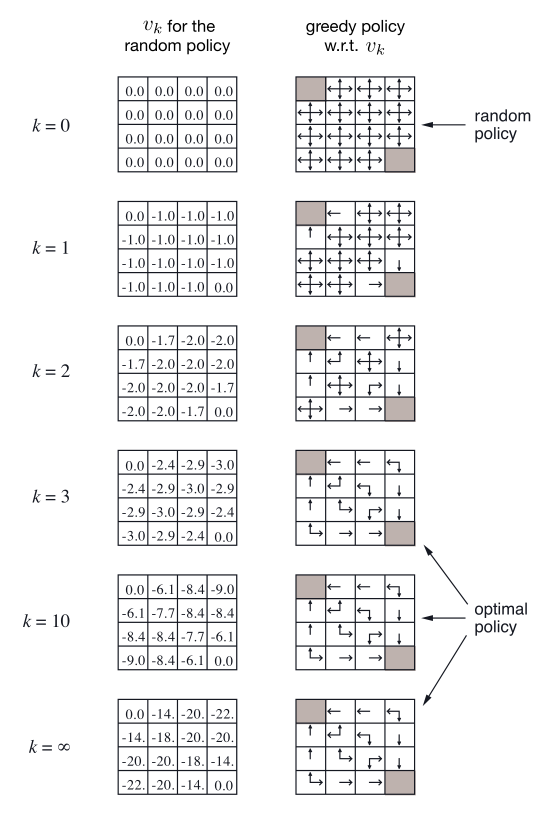
策略改进
计算价值函数的一个原因是为了找到更好的策略,我们可以知道如果从状态
一种解决方法是在状态
一个关键的准则就是这个值是大于还是小于
如果
那么我们称策略
证明过程:
到目前为止,我们已经看到了,给定一个策略及其价值函数,我可以很容易评估一个状态中某个特定动作的改变会产生怎样的后果。我们可以很自然地延伸到所有的状态和所有可能的动作,即在每个状态下根据
这种根据原策略的价值函数执行贪心算法,来构造一个更好策略的过程,称为策略改进
策略迭代
一旦一个策略

价值迭代
策略迭代算法的一个缺点是每一次迭代都涉及了策略评估,这本身就是一个需要多次遍历状态集合的迭代过程,如果策略评估是迭代进行的,那么收敛到
上面GridWorld的例子很明显就能说明,我们可以提前截断策略评估的过程,在这个例子中,前三轮策略评估之后的迭代对其贪心策略没有产生影响。
事实上,由很多方式可以截断策略迭代中的策略评估步骤,一种重要的方法是:在每一次遍历后即刻停止策略评估(对每个状态进行一次更新)。该算法被称为价值迭代,可以将此表示为结合了策略改进与截断策略评估的简单更新公式:
价值迭代与策略评估的更新公式几乎完全相同。
理论上价值迭代需要迭代无限次才能收敛,事实上,如果一次遍历中仅发生一些细微的变化,那么就可以停止。

广义策略迭代
策略迭代包括两个同时进行的相互作用的流程,一个使得价值函数与当前策略一致(策略评估),另一个根据当前价值函数贪心地更新策略(策略改进)。
用广义策略迭代(GPI)一词来指代让策略评估和策略改进相互作用地一般思路,几乎所有的强化学习算法都可以被描述成广义策略迭代算法:
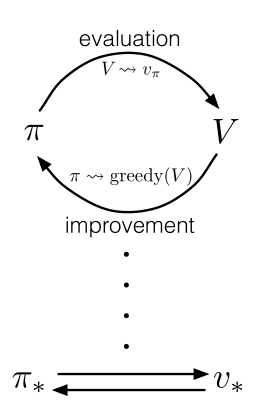
价值函数只有在与当前策略一致时才稳定,并且策略只有在对当前价值函数是贪心策略时才稳定。
可以将GPI的评估与改进流程看作竞争与合作。竞争是指它们朝着相反的方向前进,让策略对价值函数贪心通常会使价值函数与当前策略不再匹配,而使价值函数与策略一致通常会导致策略不再贪心。合作是指从长远看,这两个流程相互作用以找到一个联合解决方案:最优价值函数和一个最优策略。
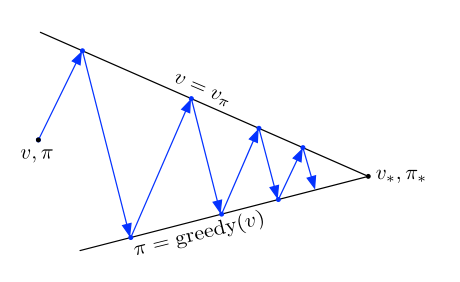
动态规划的效率
DP算法有时会因为维度灾难而被认为缺乏实用性。集合太大确实会带来一些困难,但是这是问题本身的困难,而非DP作为一种解法所带来的困难。事实上,相比于直接搜索和线性规划,DP更加适合解决大规模状态空间的问题。
- 标题: 强化学习之动态规划
- 作者: Oliver xu
- 创建于 : 2020-08-19 23:06:50
- 更新于 : 2025-07-11 21:08:03
- 链接: https://blog.oliverxu.cn/2020/08/19/强化学习之动态规划/
- 版权声明: 本文章采用 CC BY-NC-SA 4.0 进行许可。